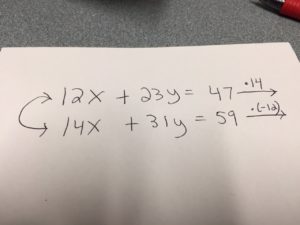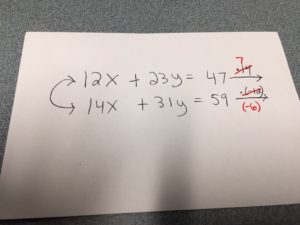A Student Shares a Great Observation
Today in my elementary algebra class we were reviewing solving systems of equations by addition or substitution. We were going over a system where students were having trouble determining what number to multiply each equation by in the system in order to eliminate the variable x. We had been discussing that the goal is to find the LCM of 12 and 14, but I told them that on exam day they could always fall back on multiplying each equation by the coefficient of x in the other equation (while making sure that produced one positive coefficient and one negative coefficient).
I then showed the class that they could find the LCM by finding the prime factorization of 12 and 14, gathering the results in a Venn diagram. Multiplying 6 by 2 by 7, the LCM is 84.
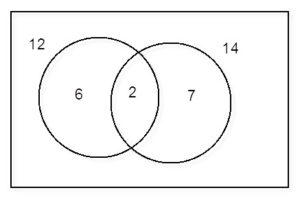 I finally showed them where the Venn diagram tells us that we can multiply 12 by 7 to get 84, and 14 by -6 to get -84.
I finally showed them where the Venn diagram tells us that we can multiply 12 by 7 to get 84, and 14 by -6 to get -84.
One of my students pointed out to me (and the entire class) how he came to decide that he could multiply the two equations by 7 and -6. He started with 14 and -12, then divided both of those by their common factor of 2.
I loved the original thought, and repeated what he said to the entire class. I saw a lot of heads shaking in approval, and my students have a new strategy to use when the LCM does not jump out at them. It was a great day in elementary algebra!
Do you have a story about a student discovery to share? I’d love to hear from you through the contact page on my website, posting a comment, or by reaching out to me on Twitter (@georgewoodbury).
-George